Summary

窝真是太蒻了, 左偏树现在才学会 qwq.
这篇主要讲了可以实现可并堆的数据结构之一, 左偏树.(您猜为什么没有破折号
前置芝士: 二叉树, 堆 , 神仙 $\color{black}{\text{j}}\color{red}{\text{iangly}}$: 愿青龙指引你.

Link

神仙 $\color{black}{\text{j}}\color{red}{\text{iangly}}$: 模板题.
洛咕咕的板子 P3377 可并堆
洛咕咕的例题 P1456 Monkey King

Text

左偏树 什么都可以 可以干什么

左偏树可以实现可并堆.
意思就是说可以用左偏树维护很多个堆, 并可以合并它们, 单次复杂度是 $O(log_n)$.
证明复杂度:OI 选手不需要证明 窝不会.

左偏树的几个性质

首先看一张左偏树的图

, 啊不对是这个 qwq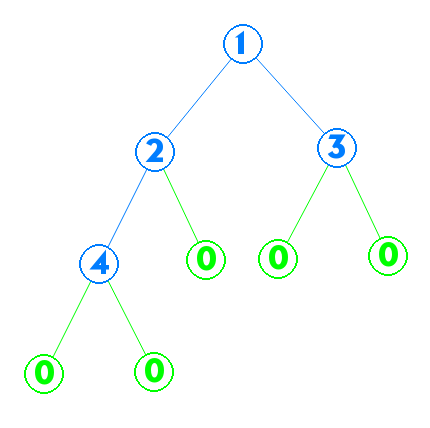

, 可以看到左偏树有这几条性质:

• 一颗左偏树是一颗二叉堆 (废话;
• 定义外节点为子节点数少于一个 (绿色) 的节点,$dis_i$ 为节点 $i$ 子树中离 $i$ 最近的节点与 $i$ 之间的边数, 则有 $dis_{ls_i} \ge dis_{rs_i}$.

如何构造和维护一颗左偏树

最简单的左偏树只有一个根, 除此以外什么都没有. 让窝们从这里开始.
Code:

val[i] = /* 一个您想它是是的随便什么东西 */, fat[1] = 1;

当需要加入新节点时, 将新节点当作一颗新的左偏树合并就好了 qwq.

接下来就是重要的合并操作, 现在假设要将 b 合并到 a 上.

• 如果合并会违反性质 1 或 2, 就交换 a,b;
• 如果 a 的右子树为空, 就直接把 b 接上去;
• 否则就合并 a 的右子树和 b;
• 最后检查是否符合性质, 不符合就交换 a 的左右子树.

Code:

inline int merge(int nsa, int nsb)
{
    if (!nsa || !nsb) // 如果要合并的两颗树有一颗为空
        return nsa + nsb; // 就返回另一颗的根坐标
    // 假设将b树作为a树的子树
    if (val[nsa] > val[nsb]) // 不符合性质1
        swap(nsa, nsb); // 交换a,b树
    son[nsa][1] = merge(son[nsa][1], nsb); // 将a的右子树设为a的右子树与b树合并后新的根
    if (dis[son[nsa][0]] < dis[son[nsa][1]]) // 不符合性质2
        swap(son[nsa][0], son[nsa][1]); // 交换a的左右子树
    fat[nsa] = fat[son[nsa][0]] = fat[son[nsa][1]] = nsa; // 这一句的作用后面讲qwq
    dis[nsa] = dis[son[nsa][1]] + 1; // 维护性质2
    return nsa; // 返回合并完成后的根
}

怎么搞 一 下这些操作呢

首先是加入一个节点:
先创建一颗只有一个值为待加入的值的节点, 然后把它合并到要加入的那个堆里面就好了.
Code:

 // 显然这么搞一下,再这么搞一下就可以了qwq
 // 显然窝只是不想放代码qwq

然后是删除:
显然窝们只会从堆顶删除, 所以要删除的节点是一定没有父亲的 qwq,
把这个节点的左右子树的父亲设为自己, 再合并它的左右子树. 然后就没有然后了.
Code:

inline void pop(int nps)
{
    val[nps] = -1; // 表示这个节点已经被删除了,在查询的时候会用到qwq
    fat[son[nps][0]] = son[nps][0], fat[son[nps][1]] = son[nps][1];
    fat[nps] = merge(son[nps][0], son[nps][1]);
}

但是窝 TLE 了应该怎么办呢

窝之前给出的写法复杂度是不对的 ( 那岂不是白看!qwq. 要想有正确的复杂度, 还必须要有一个 富有神秘主义色彩的 路径压缩.
先看代码,Code:

inline int getf(int nps)
{
    return nps == fat[nps] ? nps : fat[nps] = getf(fat[nps]);
}

啊咧这不是和并查集的 完 全 一 致 一样嘛. 然后窝们就可以讲一下merge中这一句

fat[nsa] = fat[son[nsa][0]] = fat[son[nsa][1]] = nsa; // 这一句的作用后面讲qwq

的作用了: 在合并的时候会有父子关系的改变, 所以需要这一句. 具体讲的话 窝不会 会很复杂, 就不讲了 qwq.

然后是例题的完整代码啦

Code:

#include <cstdio>
#include <iostream>
using namespace std;

int n, m, rot, in0, in1;
int val[100005], dis[100005], son[100005][2];
int fat[100005];

inline int getf(int nps)
{
    return nps == fat[nps] ? nps : fat[nps] = getf(fat[nps]);
}

inline int merge(int nsa, int nsb)
{
    if (!nsa || !nsb)
        return nsa + nsb;
    if (val[nsa] > val[nsb] || (val[nsa] == val[nsb] && nsa > nsb))
        swap(nsa, nsb);
    son[nsa][1] = merge(son[nsa][1], nsb);
    if (dis[son[nsa][0]] < dis[son[nsa][1]])
        swap(son[nsa][0], son[nsa][1]);
    fat[nsa] = fat[son[nsa][0]] = fat[son[nsa][1]] = nsa;
    dis[nsa] = dis[son[nsa][1]] + 1;
    return nsa;
}

inline void pop(int nps)
{
    val[nps] = -1;
    fat[son[nps][0]] = son[nps][0], fat[son[nps][1]] = son[nps][1];
    fat[nps] = merge(son[nps][0], son[nps][1]);
}

int main()
{
    dis[0] = -1;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &val[i]), fat[i] = i;
    while (m--)
    {
        scanf("%d%d", &in0, &in1);
        if (in0 - 1)
        {
            if (val[in1] == -1)
                printf("-1\n");
            else
                printf("%d\n", val[getf(in1)]), pop(getf(in1));
        }
        else
        {
            scanf("%d", &in0);
            if (val[in0] == -1 || val[in1] == -1)
                continue;
            if (getf(in0) != getf(in1))
                fat[getf(in0)] = fat[getf(in1)] = merge(getf(in0), getf(in1));
        }
    }
    return 0;
}