Summary

动态邻接表相关

Text

链表是什么

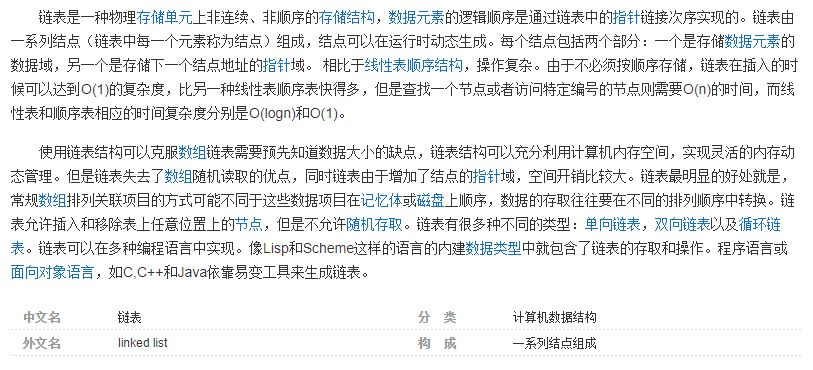
摘自 百度百科

链表是一种数据结构, 效果类似于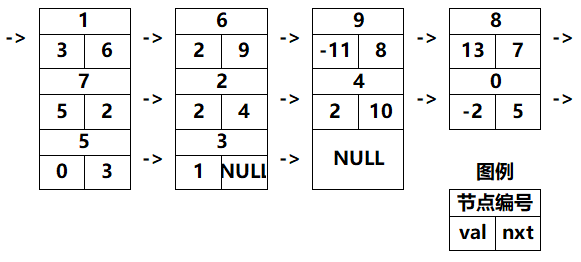

链表的作用 (之一)

存图, 在稀疏图上有奇效 (就是邻接表)

栗子: 一张有 100 个节点,1000 条边的图, 用数组存

int mp[100][100];

用链表存

struct str
{
    int fin, len;
    str *nxt;
} mp[1000], *f[100];
int cnt;

大小差距极其明显 emmm...

静态链表的写法

略

邻接表的写法

声明

struct str
{
    int fin, len;
    str *nxt;
} mp[1000], *f[100];
int cnt;

插入边

void insert(int orf /*始点*/, int nif /*终点*/, int nel /*边权*/)
{
    mp[++cnt].fin = nif;
    mp[cnt].len = nel;
    mp[cnt].nxt = f[orf];
    f[orf] = &mp[cnt];
}

遍历一个点的所有出边

for (str *i = f[/*点的编号*/]; i; i = i->nxt)

动态链表与邻接表

申明

struct str
{
    int fin, len;
    str *nxt;
} * f[220];

使用 new 动态加边, 实现内存动态分配. 用法

str */*指针名*/ = new /*指向元素类型*/;

具体到邻接表里面, 则是

void insert(int orf, int nif, int nel)
{
    str *wen = new str();
    wen->fin = nif;
    wen->len = nel;
    wen->nxt = f[orf];
    f[orf] = wen;
}

使用 delete 删边, 实现内存回收. 用法

delete /*指针名*/;

具体到邻接表里面, 则是

inline void remove(int orf, int nif)
{
    if (f[orf]->fin == nif)
    {
        str *i = f[orf];
        f[orf] = i->nxt;
        delete i;
        return;
    }
    for (str *i = f[orf], *j = i->nxt; j; i = j, j = j->nxt)
    {
        if (j->fin == nif)
        {
            i->nxt = j->nxt;
            delete j;
        }
    }
}

栗子:

#include <cstdio>
using namespace std;

struct str
{
    int fin, len;
    str *nxt;
} * f[100];
int n, m, in1, in2, in3, in4;

inline void insert(int orf, int nif, int nel)
{
    str *wen = new str();
    wen->fin = nif;
    wen->len = nel;
    wen->nxt = f[orf];
    f[orf] = wen;
}

inline void remove(int orf, int nif)
{
    if (f[orf]->fin == nif)
    {
        str *i = f[orf];
        f[orf] = i->nxt;
        delete i;
        return;
    }
    for (str *i = f[orf], *j = i->nxt; j; i = j, j = j->nxt)
    {
        if (j->fin == nif)
        {
            i->nxt = j->nxt;
            delete j;
        }
    }
}

int main()
{
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
    scanf("%d%d", &n, &m);
    while (m--)
    {
        scanf("%d", &in1);
        switch (in1)
        {
        case 1:
            scanf("%d%d%d", &in2, &in3, &in4);
            insert(in2, in3, in4);
            break;
        case 2:
            scanf("%d%d", &in2, &in3);
            remove(in2, in3);
            break;
        case 3:
            for (int i = 1; i <= n; i++)
            {
                printf("[%d]", i);
                for (str *j = f[i]; j; j = j->nxt)
                    printf("->[%2d|%2d]", j->fin, j->len);
                printf("\n");
            }
            printf("--------------------\n");
            break;
        }
    }
    return 0;
}

in.txt

5 11
1 1 3 10
1 3 2 7
1 4 5 9
1 2 4 -1
3
2 2 4
3
1 2 4 1
1 1 5 7
1 5 1 3
3

out.txt

[1]->[ 3|10]
[2]->[ 4|-1]
[3]->[ 2| 7]
[4]->[ 5| 9]
[5]
--------------------
[1]->[ 3|10]
[2]
[3]->[ 2| 7]
[4]->[ 5| 9]
[5]
--------------------
[1]->[ 5| 7]->[ 3|10]
[2]->[ 4| 1]
[3]->[ 2| 7]
[4]->[ 5| 9]
[5]->[ 1| 3]
--------------------

栗子:P1359

Reference

• https://www.cnblogs.com/wanqieddy/p/4372033.html
• https://blog.csdn.net/nyist_zxp/article/details/80810742
• https://blog.csdn.net/qq544529563/article/details/14714387
• https://blog.csdn.net/u010234441/article/details/83310503
• https://blog.csdn.net/qq_35750858/article/details/53184137
• https://blog.csdn.net/sinat_38816924/article/details/78482793