打字大赛 游记
Summary
比赛名字已经彻底暴露了问题所在.
我太蒻啦!
Links
[这是正式比赛的游记(空链接, 因为窝是鸽子)]()
Text
L1
01 温度转换表
Problem
输入 2 个正整数 lower 和 upper(lower≤upper≤100), 请输出一张取值范围为 [lower,upper], 且每次增加 2 华氏度的华氏 - 摄氏温度转换表.
温度转换的计算公式:
C=5×(F−32)/9, 其中:C 表示摄氏温度,F 表示华氏温度.Input Format
在一行中输入 2 个整数, 分别表示 lower 和 upper 的值, 中间用空格分开.
Output Format
第一行输出:"fahr celsius".
接着每行输出一个华氏温度 fahr(整型, 占 4 个字符宽度, 左对齐) 与一个摄氏温度 celsius(占据 6 个字符宽度, 靠右对齐, 保留 1 位小数).
若输入的范围不合法, 则输出 "Invalid.".
Input sample 1
32 35Output sample 1
fahr celsius
32 0.0
34 1.1Input sample 2
40 30Output sample 2
Invalid.Code
#include <cstdio>
using namespace std;
int l, u;
int main()
{
freopen("L1-01.in", "r", stdin);
freopen("L1-01.out", "w", stdout);
scanf("%d%d", &l, &u);
if (l > u || l > 100 || u > 100)
{
printf("Invalid.");
return 0;
}
printf("fahr celsius\n");
for (; l <= u; l += 2)
{
printf("%d", l);
if (l < 10)
printf(" ");
else if (l < 100)
printf(" ");
else
printf(" ");
printf("%6.1lf\n", 5.0 * ((double)l - 32.0) / 9.0);
}
return 0;
}02 龟兔赛跑
Problem
乌龟与兔子进行赛跑, 跑场是一个矩型跑道, 跑道边可以随地休息. 乌龟每分钟可以前进 3 米, 兔子每分钟前进 9 米; 兔子嫌乌龟跑得慢, 觉得肯定能跑赢乌龟, 于是, 每跑 10 分钟就回头看一下乌龟, 若发现自己超过乌龟, 就在路边休息, 每次休息 30 分钟, 否则继续跑 10 分钟; 而乌龟非常努力, 一直跑, 不休息. 假定乌龟与兔子在同一起点同一时刻开始起跑, 请问 T 分钟后乌龟和兔子谁跑得多?
Input Format
在一行中给出一个正整数, 表示比赛时长 T(分钟).
Output Format
在一行中输出比赛的结果: 乌龟赢时输出 "@\_@", 兔子赢时输出 "^\_^", 平局则输出 "-_-"; 后跟一空格, 再输出胜利者跑完的路程(米).
Input sample
242Output sample
@_@ 726Code
#include <cstdio>
using namespace std;
int T, r, t, i;
int main()
{
freopen("L1-02.in", "r", stdin);
freopen("L1-02.out", "w", stdout);
scanf("%d", &T);
for (i = 1; i <= T; i++)
{
t += 3;
r += 9;
if (i % 10 == 0 && r > t)
t += 90, i += 30;
}
while (i -1> T)
t -= 3, i--;
if (t > r)
printf("@_@ %d", t);
else if (t < r)
printf("^_^ %d", r);
else
printf("-_- %d", r);
return 0;
}03 几点几分
Problem
有时候人们用四位数字表示一个时间, 比如 1106 表示 11 点零 6 分. 现在, 请编写程序, 根据起始时间和流逝的时间计算出终止时间.
读入两个数字, 第一个数字 T 以这样的四位数字表示当前时间, 第二个数字表示分钟数 P, 计算当前时间 T 经过那么 P 分钟后是几点几分, 结果也表示为四位数字 (当小时为个位数时为 3 位数字).Input Format
输入在一行中给出 2 个整数, 分别是四位数字表示的起始时间, 以及流逝的分钟数, 其间以空格分隔. 注意: 起始时间中的小时为个位数时没有前导的零, 即 5 点 30 分表示为 530; 流逝的分钟数可能超过 60, 也可能是负数.
Output Format
输出四位数字表示的终止时间. 题目保证起始时间和终止时间在同一天内.
Input sample
1120 110Output sample
1310Code
#include <cstdio>
using namespace std;
int s, sh, sm, p, ph, pm;
bool f;
int main()
{
freopen("L1-03.in", "r", stdin);
freopen("L1-03.out", "w", stdout);
scanf("%d%d", &s, &p);
sh = s / 100, sm = s % 100;
if (p < 0)
p = -p, f = true;
ph = p / 60, pm = p % 60;
if (f)
printf("%d%02d", sh - ph + (sm - pm - 60) / 60, (sm - pm + 60) % 60);
else
printf("%d%02d", sh + ph + (sm + pm) / 60, (sm + pm) % 60);
return 0;
}04 A-B
Problem
请编写程序计算 A−B. 不过麻烦的是,A 和 B 都是字符串.A−B 是指从字符串 A 中把字符串 B 所包含的字符全部删掉, 剩下的字符所组成的字符串.
Input Format
输入分为 2 行, 分别给出字符串 A 和 B(长度都不超过 10^4, 并且保证每个字符串都是由可见的 ASCII 码和空白字符组成).
Output Format
在一行中打印出 A−B 的结果字符串.
Input sample
Things do not change; we change.
aei TouOutput sample
hngsdntchng;wchng.Code
#include <cstdio>
#include <cstring>
using namespace std;
char a[10020], b[10020];
bool f[1000];
int main()
{
freopen("L1-04.in", "r", stdin);
freopen("L1-04.out", "w", stdout);
gets(a), gets(b);
for (int i = 0; b[i]; i++)
f[(int)b[i]] = true;
for (int i = 0; a[i]; i++)
if (!f[(int)a[i]])
printf("%c", a[i]);
return 0;
}05 移动机器人
Problem
机器人按照给定的指令在网格中移动, 指令有以下四种:
N 向北 (上) 移动
S 向南(下) 移动
E 向东(右) 移动
W 向西(左) 移动
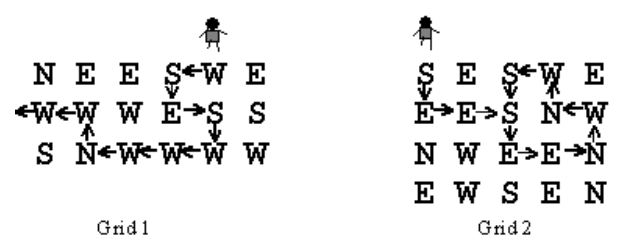
如下图所示, 在网格 1 中, 机器人初始位于网格第 1 行第 5 列, 按照网格中的指令, 机器人在走出网格前需要 10 步. 在网格 2 中, 机器人初始位于网格第 1 行第 1 列, 按照网格中的指令, 机器人将进入一个循环, 永远走不出网格.
假定机器人初始时刻总是在网格第一行的某一列上, 请你写一个程序确定机器人能否走出网格, 以及走出网格需要的步数.
Input Format
有多组数据, 每组数据的第一行为 3 个正整数, 分别表示网格行数 N, 列数 M 和初始时刻机器人所在的列 C(从网格最左边开始, 从 1 开始计数). 每个网格的行数和列数均不超过 10. 接下来是 N 行指令, 指令只包含 N,S,E 和 W 四种, 所有指令之间没有空格. 当 N,M 和 C 均为 0 时表示输入结束.
Output Format
对每组数据输出一行结果, 如果机器人可以走出网格, 输出其走出网格需要的步数; 如果机器人不能走出网格, 输出 "no".
Input sample
3 6 5
NEESWE
WWWESS
SNWWWW
4 5 1
SESWE
EESNW
NWEEN
EWSEN
0 0 0Output sample
10
noCode
#include <cstdio>
#include <cstring>
using namespace std;
int n, m, x, y, t;
char mp[1005][1005];
bool v[1005][1005], f;
int main()
{
freopen("L1-05.in", "r", stdin);
freopen("L1-05.out", "w", stdout);
while ((scanf("%d%d%d", &n, &m, &y)) != EOF && (n ||M|| y))
{
memset(v, 0, sizeof(v)), f = false, x = 1, t = 0;
for (int i = 1; i <= n; i++)
{
scanf("\n");
for (int j = 1; j <= m; j++)
mp[i][j] = getchar();
}
while (!v[x][y])
{
v[x][y] = true;
if (x < 1 || x >n|| y < 1 || y > m)
{
printf("%d\n", t);
f = true;
break;
}
if (mp[x][y] == 'N')
x--;
else if (mp[x][y] == 'S')
x++;
else if (mp[x][y] == 'E')
y++;
else
y--;
t++;
}
if (!f)
printf("no\n");
}
return 0;
}06 魔方阵
Problem
请编写程序输出 n 阶魔方阵 (n 为奇数).Dole Rob 算法生成 n 阶(n 为奇数) 魔方阵 (各行, 列, 对角线数字之和相等) 的过程为: 从 1 开始, 按如下方法依次插入各自然数, 直到 n^2 为止:
a. 在第一行的正中插入 1;
b. 新位置应当处于最近插入位置的右上方, 若该位置已超出方阵的上边界, 则新位置取应选列的最下一个位置; 若超出右边界, 则新位置取应选行的最左一个位置;
c. 若最近插入的元素是 n 的整数倍, 则选同列的下一行位置为新位置.
Input Format
为一个整数 n(≤20), 表示方阵的阶.
Output Format
若 n 为偶数, 则在一行上输出 "Wrong input!"; 若 n 为奇数, 则输出 n 行, 每行 n 个整数表示 n 阶魔方阵, 整数之间以 1 个空格分隔, 每行第一个整数之前, 最后 1 个整数之后无空格.
Input sample
3Output sample
8 1 6
3 5 7
4 9 2Code
#include <cstdio>
#include <cstring>
using namespace std;
int n, x = 1, y, mp[30][30];
int main()
{
freopen("L1-06.in", "r", stdin);
freopen("L1-06.out", "w", stdout);
scanf("%d", &n);
if (!(n & 1))
{
printf("Wrong input!");
return 0;
}
y = (n >> 1) + 1;
for (int i = 1; i <=N* n; i++)
{
mp[x][y] = i;
if (i %N== 0)
{
x++;
continue;
}
x--, y++;
if (x < 1)
x = n;
else if (x > n)
x = 1;
if (y < 1)
y = n;
else if (y > n)
y = 1;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < n; j++)
printf("%d ", mp[i][j]);
printf("%d\n", mp[i][n]);
}
return 0;
}L2
01 红色警报
Problem
战争中保持各个城市间的连通性非常重要. 本题要求你编写一个报警程序, 当失去一个城市导致国家被分裂为多个无法连通的区域时, 就发出红色警报. 注意: 若该国本来就不完全连通, 是分裂的 K 个区域, 而失去一个城市并不改变其他城市之间的连通性, 则不要发出警报.
Input Format
输入在第一行给出两个正整数 N(≤500)和 M(≤5000), 分别为城市个数 (于是默认城市从 0 到 N - 1 编号) 和连接两城市的通路条数. 随后 M 行, 每行给出一条通路所连接的两个城市的编号, 其间以 1 个空格分隔. 在城市信息之后给出被攻占的信息, 即一个正整数 K 和随后的 K 个被攻占的城市的编号.
注意: 输入保证给出的被攻占的城市编号都是合法的且无重复, 但并不保证给出的通路没有重复.
Output Format
对每个被攻占的城市, 如果它会改变整个国家的连通性, 则输出“Red Alert: City K is lost!”, 其中 K 是该城市的编号; 否则只输出“City K is lost.”即可. 如果该国失去了最后一个城市, 则增加一行输出“Game Over.”.
Input sample
5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3Output sample
City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.Code
#include <cstdio>
using namespace std;
int main()
{
freopen("L2-01.in", "r", stdin);
freopen("L2-01.out", "w", stdout);
printf("City 1 is lost.\nCity 2 is lost.Red Alert: City 0 is lost!\nCity 4 is lost.\nCity 3 is lost.\nGame Over.");
return 0;
}02 月饼
Problem
月饼是中国人在中秋佳节时吃的一种传统食品, 不同地区有许多不同风味的月饼. 现给定所有种类月饼的库存量, 总售价, 以及市场的最大需求量, 请你计算可以获得的最大收益是多少.
注意: 销售时允许取出一部分库存. 样例给出的情形是这样的: 假如我们有 3 种月饼, 其库存量分别为 18,15,10 万吨, 总售价分别为 75,72,45 亿元. 如果市场的最大需求量只有 20 万吨, 那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼, 以及 5 万吨第 3 种月饼, 获得 72+45/2=94.5(亿元).
Input Format
每个输入包含 1 个测试用例. 每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数, 以及不超过 500(以万吨为单位)的正整数 D 表示市场最大需求量. 随后一行给出 N 个正数表示每种月饼的库存量 (以万吨为单位); 最后一行给出 N 个正数表示每种月饼的总售价(以亿元为单位). 数字间以空格分隔.
Output Format
对每组测试用例, 在一行中输出最大收益, 以亿元为单位并精确到小数点后 2 位.
Input sample
3 20
18 15 10
75 72 45Output sample
94.50Thought
水题.
因为可以不把一种卖完, 所以可以直接按照单价排降序, 然后一个个扫过去, 能卖完就卖完, 不能就尽可能多地卖, 然后输出答案, 退出 (因为若是此时卖不完证明剩余需求量已经不够了, 尽可能多就是把剩下需求全部满足).
值得注意的是排序也可以用operator, 但是写起来很麻烦, 由于这次比赛题多, 所以牺牲了一点运行时间换来了更多编程时间.
Code
#include <algorithm>
#include <cstdio>
using namespace std;
struct mc
{
int sto, mon;
double eac;
} mp[1005];
int n, d;
double ans;
bool cmp(mc a, mc b)
{
return a.eac > b.eac;
}
int main()
{
freopen("L2-02.in", "r", stdin);
freopen("L2-02.out", "w", stdout);
scanf("%d%d", &n, &d);
for (int i = 0; i < n; i++)
scanf("%d", &mp[i].sto);
for (int i = 0; i < n; i++)
scanf("%d", &mp[i].mon), mp[i].eac = (double)mp[i].mon / (double)mp[i].sto;
sort(mp, mp + n, cmp);
for (int i = 0; i < n; i++)
{
if (mp[i].sto > d)
{
ans += mp[i].eac * (double)d;
break;
}
ans += (double)mp[i].mon;
d -= mp[i].sto;
}
printf("%.2lf", ans);
return 0;
}